Chapter 9 Notation

In this chapter we will use summation notation. If you are not familiar with summation notation, we present a brief overview here.

Consider a scenario where we have the IQ data for three participants We use the N symbol to represent the number of participants. Because we have three participants N = 3. The data for these participants is illustrated in Figure 9.1.

Notice how each person in the data set can be represented by the variable X: the first person by \(X_1\), the second by \(X_2\), and the third by \(X_3\). Often we refer to individuals in a data set by using the variable X accompanied by a subscript (e.g., 1, 2, 3, etc.).

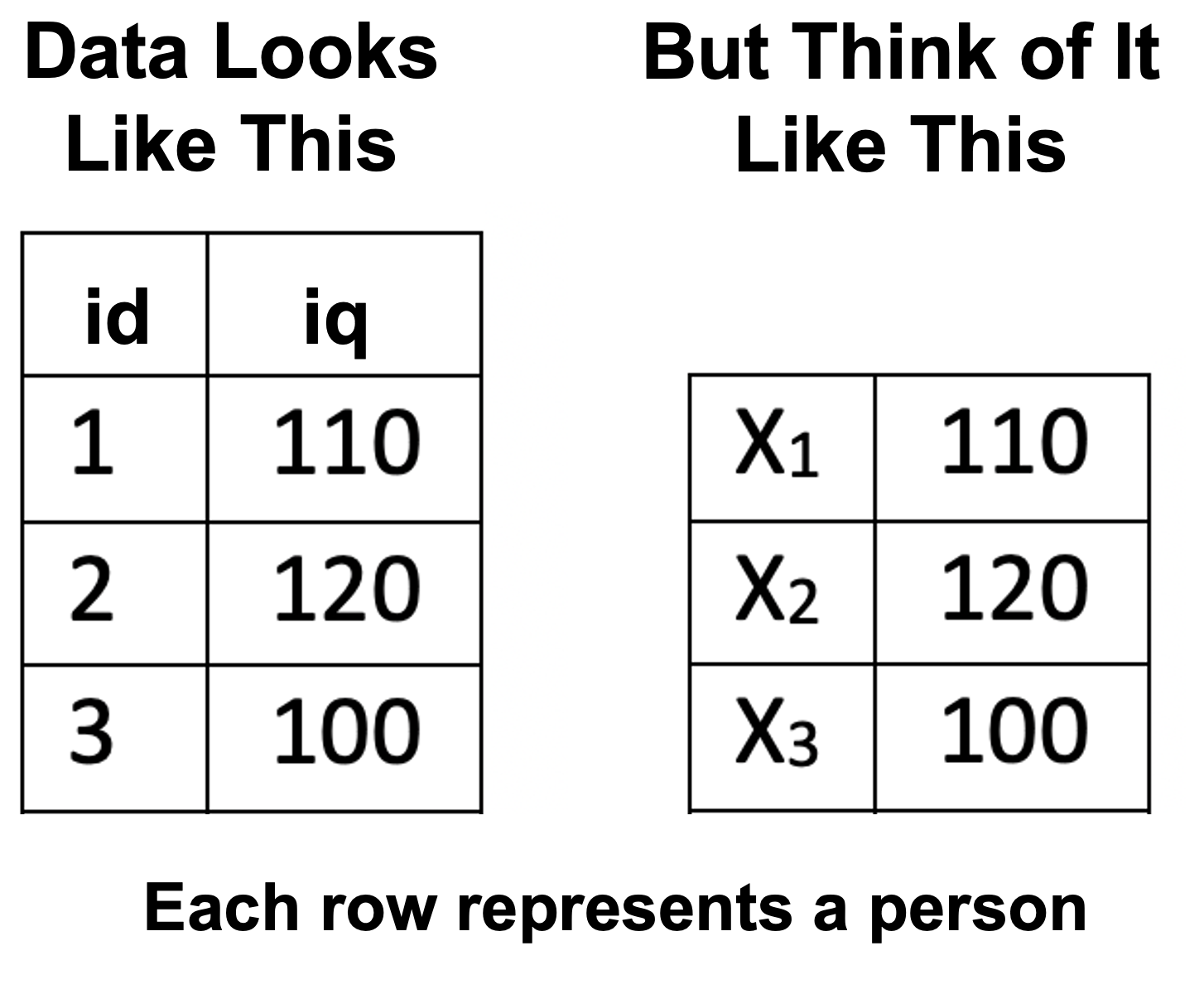
FIGURE 9.1: Data for understanding summation notation

Referring to participants using the variable X and subscript is valuable because it can be used in conjunction with the sigma (i.e., \(\Sigma\)) symbol for summation. Consider the example below in which we use the summation notation to indicate that we want to add all the X values (representing IQ) for the participants. We use a lower case \(i\) to represent all possible subscript values. The notation, \(i\) = 1, below the \(\Sigma\) symbol indicates that we should start with participant 1. The notation, N, above the \(\Sigma\) symbol indicates that we should iterate \(i\) up to the value indicated by N; in this case 3, because there are three participants.

\[ \begin{aligned} \sum_{i=1}^{N} X_i &= X_1 + X_2 + X_3\\ &= 110 + 120 + 100 \\ &= 330 \end{aligned} \]

Sometimes, to simplify the notation, the numbers above and below the \(\Sigma\) symbol are omitted. Likewise, the \(i\) subscript is omitted. There is a general understanding that when these components of the notation are omitted the version of the notation above is implied.

\[ \begin{aligned} \sum{X} &= X_1 + X_2 + X_3\\ &= 110 + 120 + 100\\ &= 330 \end{aligned} \]

Calculating a mean. The full version of the notation can be used to indicate how an average/mean is calculated.

\[ \begin{aligned} \bar{X} &= \frac{\sum_{i=1}^{N} X_i}{N} \\ &= \frac{X_1 + X_2 + X_3}{3}\\ &= \frac{110 + 120 + 100}{3}\\ &= \frac{330}{3}\\ &= 110\\ \end{aligned} \]

Likewise, the concise version of the notation can be used to indicate how an average/mean is calculated.

\[ \begin{aligned} \bar{X} &= \frac{\sum{X}}{N} \\ &= \frac{X_1 + X_2 + X_3}{3}\\ &= \frac{110 + 120 + 100}{3}\\ &= \frac{330}{3}\\ &= 110\\ \end{aligned} \]

Calculating squared differences.A common task in statistics is to calculate 1) the squared difference between each person and the mean, and 2) add up those squared differences. This calculation is easily expressed with the full version of the notation.

\[ \begin{aligned} \sum_{i=1}^{N}{(X_i - \bar{X})^2} &= (X_1-\bar{X})^2 + (X_2-\bar{X})^2 + (X_3-\bar{X})^2\\ &= (110-110)^2 + (120-110)^2 + (100-110)^2\\ &= (0)^2 + (10)^2 (-10)^2 \\ &= 0 + 100 + 100 \\ &= 200 \end{aligned} \]

Likewise, the sum of the squared differences from the mean can be expressed using the concise version of the notation.

\[ \begin{aligned} \sum{(X - \bar{X})^2} &= (X_1-\bar{X})^2 + (X_2-\bar{X})^2 + (X_3-\bar{X})^2\\ &= (110-110)^2 + (120-110)^2 + (100-110)^2\\ &= (0)^2 + (10)^2 (-10)^2 \\ &= 0 + 100 + 100 \\ &= 200 \end{aligned} \]

9.1 Measurement Notation

You may be familiar with the notation typically used when making inferences from a sample to a population. Unfortunately, the notation used in Psychological Measurement is different - similar but different. For the purposes of this course we use the notation and formulas below. Notice that we use N in the denominator - that is we use the population-level variance formula - even though we are working with sample data. Typically, measurement textbooks treat the sample as our population of interest. This difference is often a source of confusion for students.

\[ \begin{aligned} \overline{X} &= \frac{\sum{X}}{N} \\ \end{aligned} \]

\[ \begin{aligned} S^2_X &= \frac{\sum{(X - \overline{X})^2}}{N} \\ \end{aligned} \]

\[ \begin{aligned} S_X &= \sqrt{\frac{\sum{(X - \overline{X})^2}}{N}} \\ \end{aligned} \]